Tips:
- AVLTree是二叉搜索树的进一步变种
- 使用在AVLTree中的类需要实现Compareable接口
- 建议先理解链表与二叉树相关知识
demo代码
理论背景
特点
- AVLTree首先是二叉搜索树
- 带有平衡条件:每个节点的左右节点的高度差值不超过1(左子数,右子树)
- 每个节点的左子树与右子树都是AVLTree
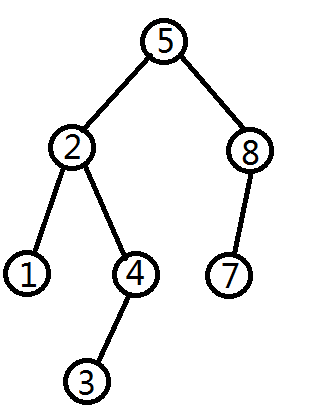
图1(AVLTree)
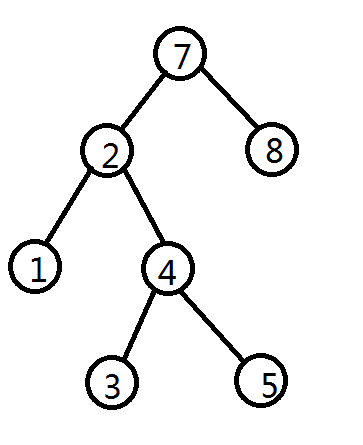
图2(非AVLTree)
旋转
节点的插入与删除都有可能会造成操作节点至根节点的所有节点的平衡信息,因此在执行插入和删除节点(单节点操作,非批量)后需要对树进行简单的修正来恢复平衡,这种操作就是旋转。
旋转一共适应四种情况:
- 对节点x的左节点的左子树进行了一次插入
- 对节点x的左节点的右子树进行了一次插入
- 对节点x的右节点的左子树进行了一次插入
- 对节点x的右节点的右子树进行了一次插入
单旋转
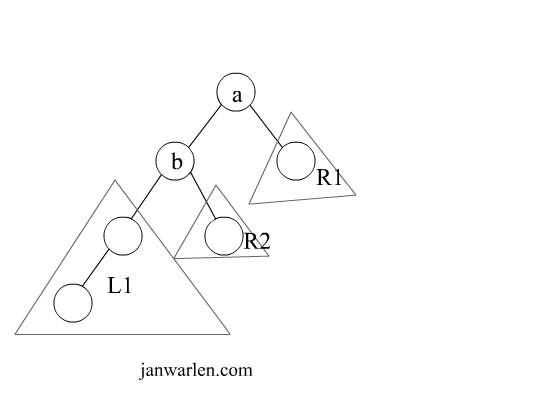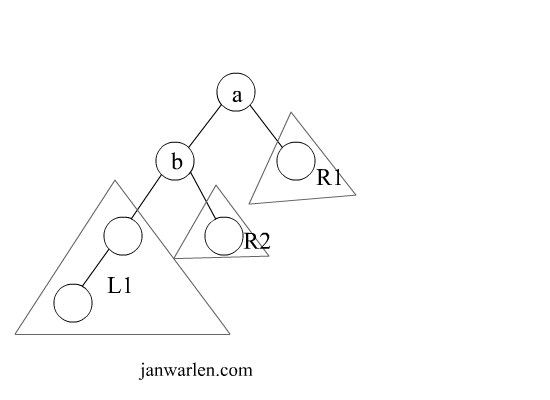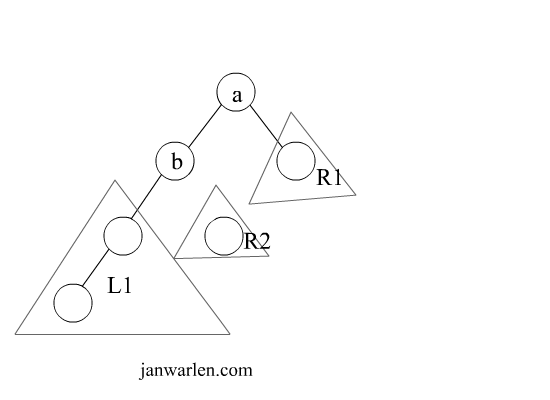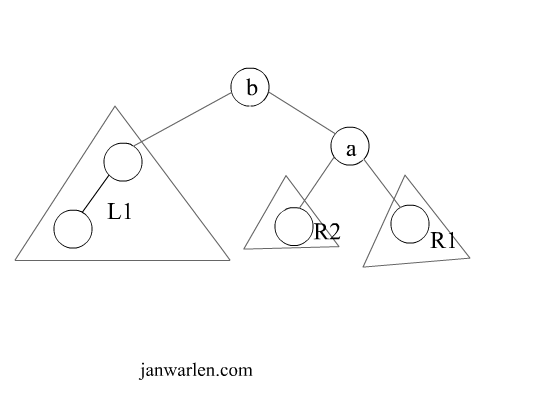
该示意图展示了第一个情况下的单旋转过程,图中节点a即情况中的节点x,L1即为左子树,至于插入的节点是L1中的哪一个则无关紧要,因为都是导致L1高度增加。因L1的高度增加,则对于节点a来说,左子树与右子树的高度差大于1,因此满足了旋转操作条件;
为了将树恢复平衡,我们需要将L1上移一层,并且将右子树R1下移一层,因此将节点b提升到根节点,此时右节点存在多个,因此根据二叉查询树的性质,子树R2是小于节点a的,因此断开节点b与子树R2的链接,将子树R2作为节点a的左子树。双旋转
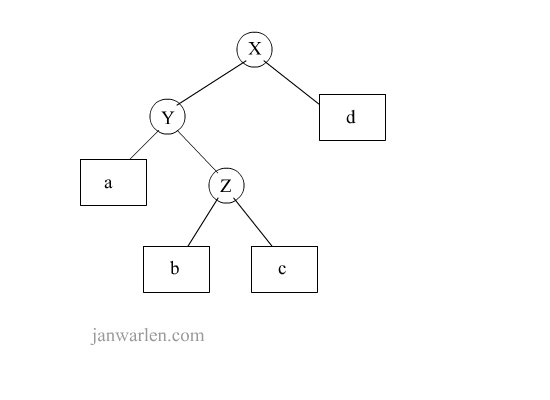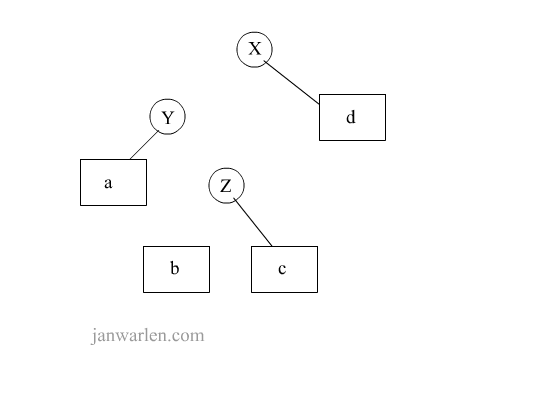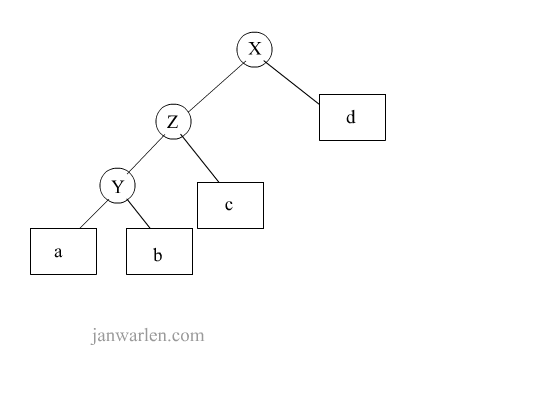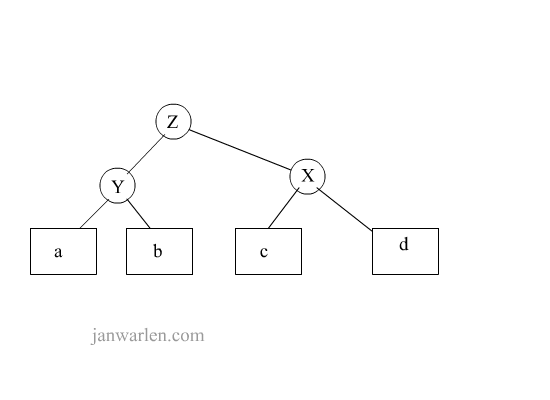
该示意图展示了双旋转解决的一种情况,实际操作中b/c仅会存在一个,因为插入b或者c时就会触发旋转操作。在示意图中,初始树无论是左单旋转还是右单旋转都无法一次平衡,因此,先进行局部旋转,待一次局部旋转后,二叉树将会转化为可单旋转的结构,此时再进行相应单旋转即可平衡二叉树。
代码实现
节点结构
首先,因为AVLTree的特性是每个节点的左右子节点的高度差不大于1(另有说法为平衡因子),因此节点除了含有常规二叉树元素还需一个元素记录改节点高度,最终设计节点结构如下:
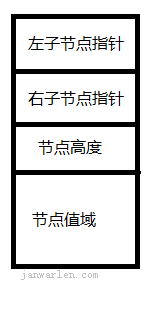
根据结构图设计节点代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| private static class Node<T> {
public Node(T element) {
this(element, null, null);
}
public Node(T element, Node<T> l, Node<T> r) {
this.element = element;
this.left = l;
this.right = r;
this.height = 0;
}
T element;
Node<T> left;
Node<T> right;
int height;
}
|
旋转操作
左单旋转
此处的左单旋转不是向左转,而是左子树进行旋转操作
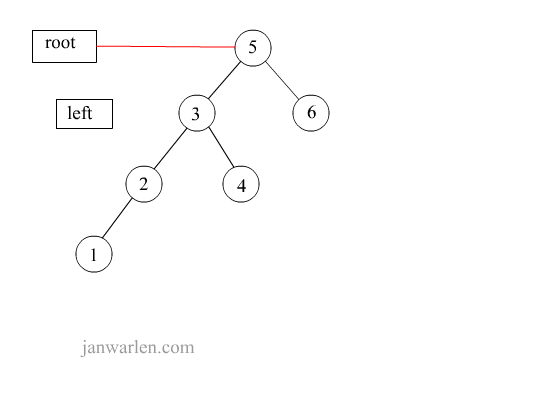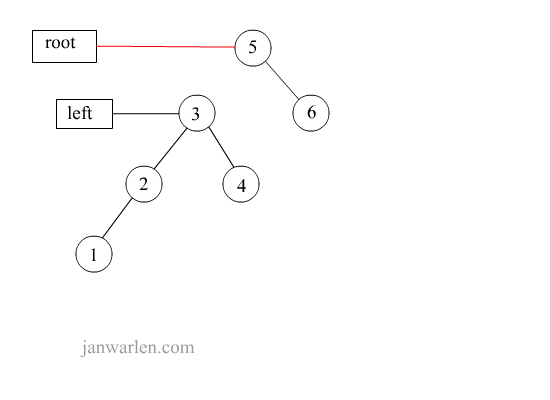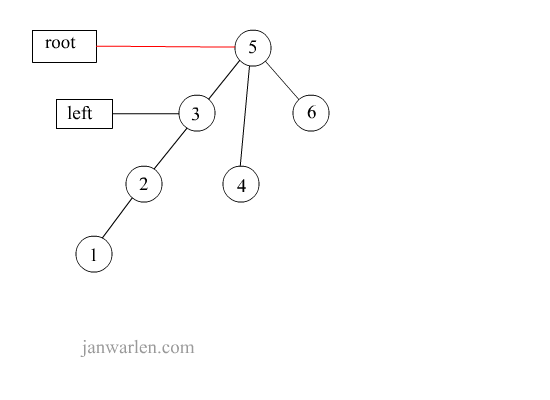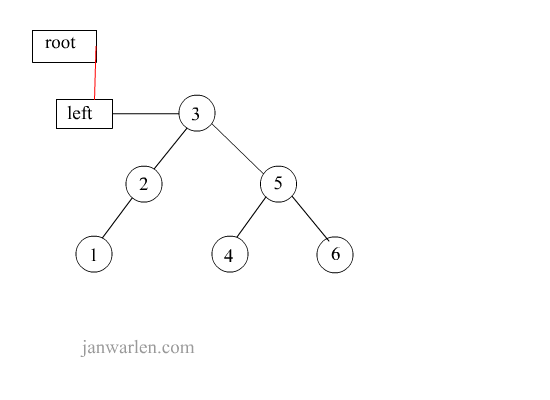
1
2
3
4
5
6
7
8
9
|
private Node<T> rotateWithLeftChild(Node<T> ele) {
Node<T> left = ele.left;
ele.left = left.right;
left.right = ele;
ele.height = Math.max(height(ele.left), height(ele.right)) + 1;
left.height = Math.max(height(left.left), height(left.right)) + 1;
return left;
}
|
右单旋转
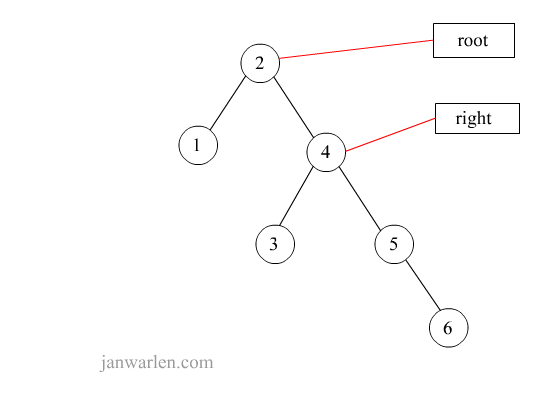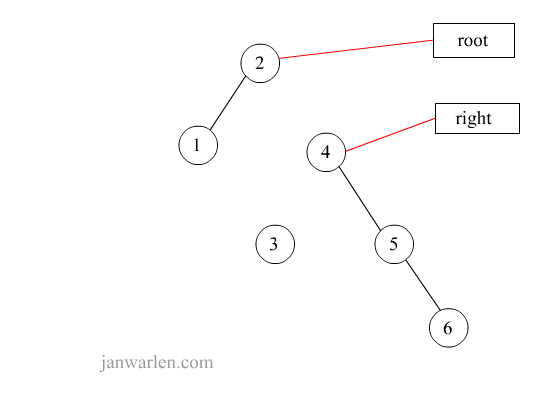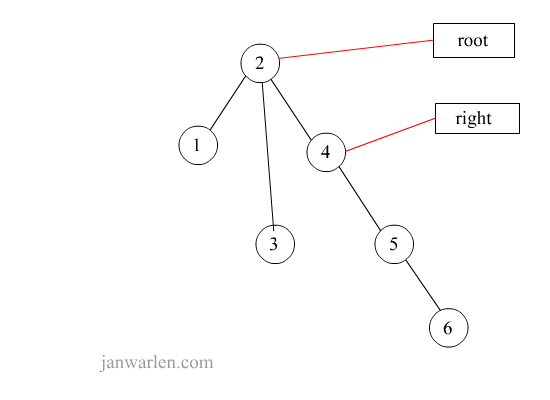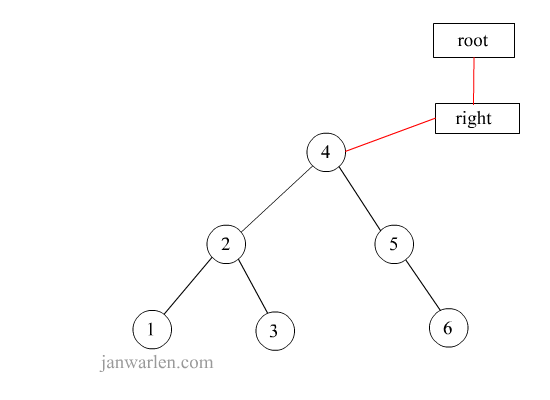
1
2
3
4
5
6
7
8
9
|
private Node<T> rotateWithRightChild(Node<T> ele) {
Node<T> right = ele.right;
ele.right = right.left;
right.left = ele;
ele.height = Math.max(height(ele.left), height(ele.right)) + 1;
right.height = Math.max(height(right.left), height(right.right)) + 1;
return right;
}
|
左双旋转
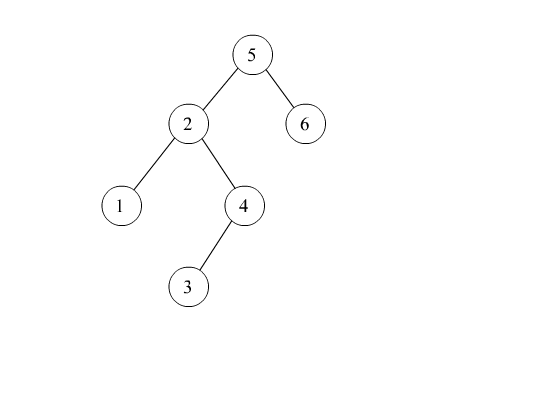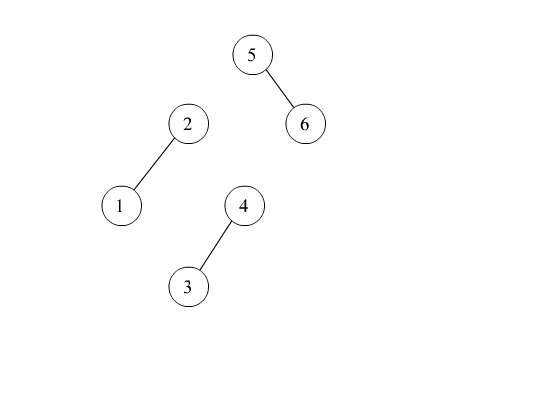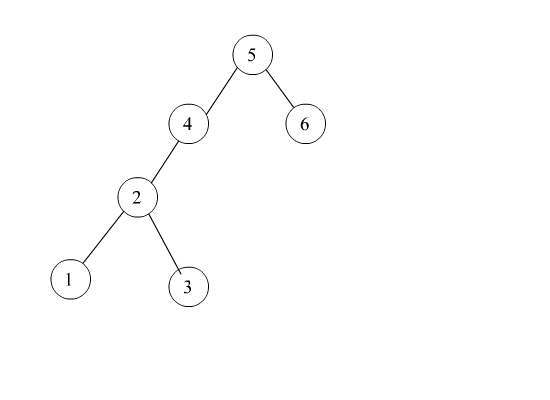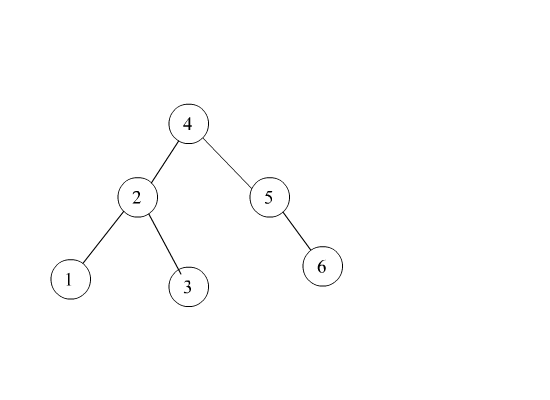
1
2
3
4
5
|
private Node<T> doubleWithLeftChild(Node<T> ele) {
ele.left = rotateWithRightChild(ele.left);
return rotateWithLeftChild(ele);
}
|
右双旋转
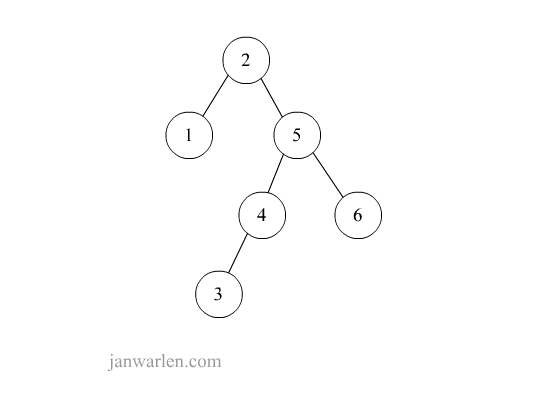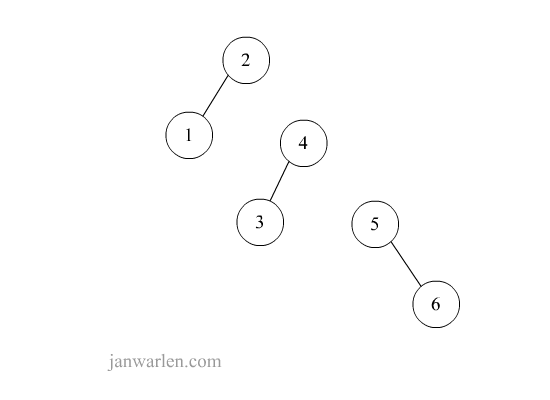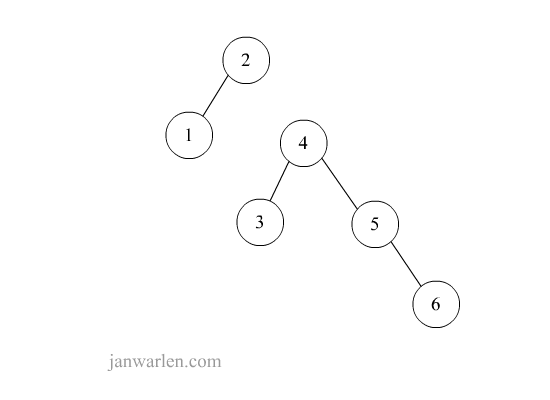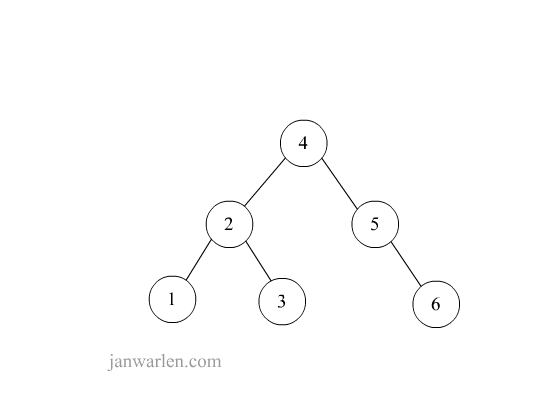
1
2
3
4
5
|
private Node<T> doubleWithRightChild(Node<T> ele) {
ele.right = rotateWithLeftChild(ele.right);
return rotateWithRightChild(ele);
}
|
平衡
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| private Node<T> balance(Node<T> ele) {
if (null == ele) {
return ele;
}
if (height(ele.left) - height(ele.right) > ALLOWED_IMBALANCE) {
if (height(ele.left.left) >= height(ele.left.right)) {
ele = rotateWithLeftChild(ele);
} else {
ele = doubleWithLeftChild(ele);
}
}
if (height(ele.right) - height(ele.left) > ALLOWED_IMBALANCE) {
if (height(ele.right.right) >= height(ele.right.left)) {
ele = rotateWithRightChild(ele);
} else {
ele = doubleWithRightChild(ele);
}
}
ele.height = Math.max(height(ele.left), height(ele.right)) + 1;
return ele;
}
|
插入
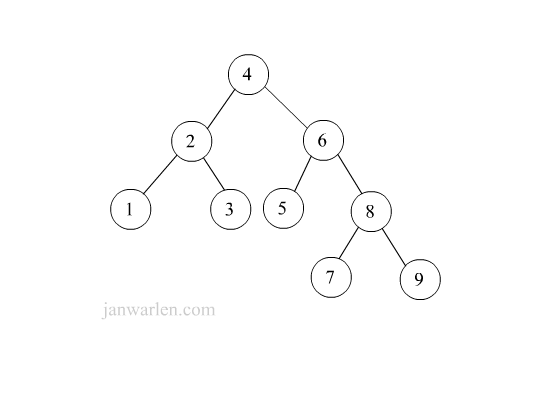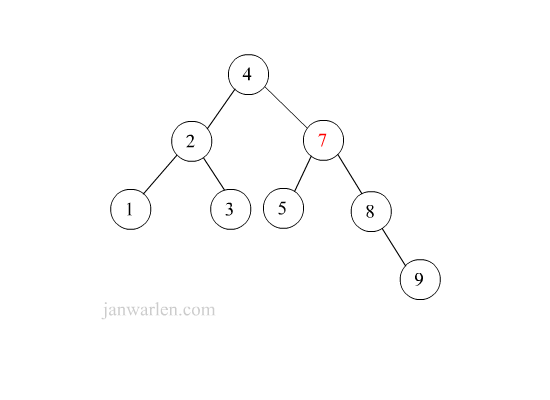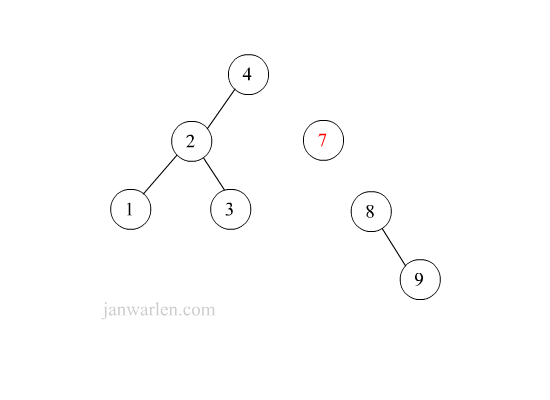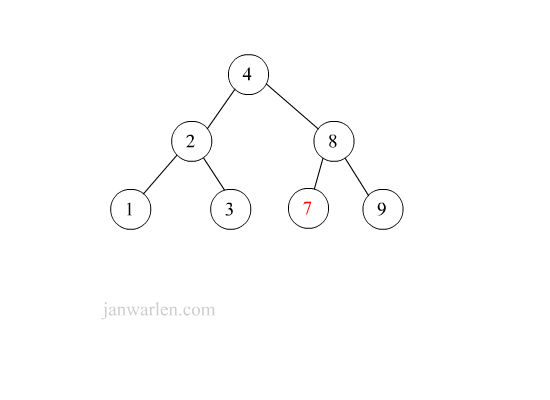
下图示例从1-9的插入过程,涵盖需要旋转情况并不全面

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public Node<T> insert(T element, Node<T> ele) {
if (null == ele) {
return new Node<T>(element);
}
Comparable<? super T> comparableEle = (Comparable<? super T>) element;
int compareRes = comparableEle.compareTo(ele.element);
if (compareRes < 0) {
ele.left = insert(element, ele.left);
} else if (compareRes > 0) {
ele.right = insert(element, ele.right);
} else {
}
return balance(ele);
}
|
删除
下图示例元素6(右子树找最小)与元素5的删除过程。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| public Node<T> remove(T element, Node<T> ele) {
if (null == ele) {
return ele;
}
Comparable<? super T> comparableEle = (Comparable<? super T>) element;
int compareRes = comparableEle.compareTo(ele.element);
if (compareRes < 0) {
ele.left = remove(element, ele.left);
} else if (compareRes > 0) {
ele.right = remove(element, ele.right);
} else if (null != ele.left && null != ele.right) {
ele.element = findMax(ele.left).element;
ele.left = remove(ele.element, ele.left);
} else {
ele = (null != ele.left) ? ele.left : ele.right;
}
return balance(ele);
}
|










